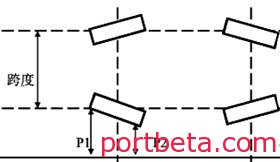
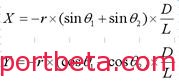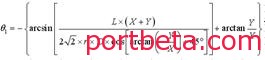图 2? 轨道示意图
纵向 0.3% (轨道的波浪度)
横向 0.3%
1.1.2? 根据FEM 欧洲起重机设计规范8.2.2.8, 小车轨道中心线同小车轨道理论中心线之差,在2 m长的轨道上,不得超过±1 mm。通常称之为轨道直线度或旁弯,参见图3。
图 3? 轨道直线度示意图
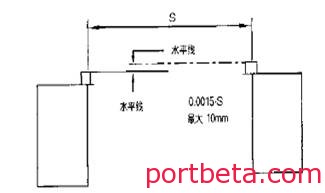
1.1.3在垂直于小车移动方向的平面内,两根小车轨道相对部位的高度差,不应超过小车轨道中心距的0.15%,且最大不超过10 mm,参见图4。
图 4? 轨道高低示意图
轨道上缘偏离理论高度的最大允许公差为±10 mm。理论高度或者是一根水平线,或者是理论拱度曲线(当有拱度时)。两条轨道的高度位置,可以相差10 mm。在2 m测量长度内的每个点上,纵向向上弯曲度应不超过+2 mm。
小车轨道的敷设,应该做到小车运行踏面水平,车轮支撑面的最大不平度,当轨道中心距不超过3 m时不大于±3 mm,轨道中心距离超过3 m时,则不大于中心距的±0.1%,参见图5。
图 5? 车轮高低差示意图
当起重机的轨道不符合上述要求时,也会形成小车跑偏啃轨现象。
1.2? 车轮直线度
对于小车车轮也有相应的规范要求。具体来说,车轮直线度可以分解为同位差与角偏差。
1.2.1 车轮的形位偏差
根据FEM8.2.2.10,两条轨道上相对车轮的轴孔轴线,如果车轮装在台车上则为未翘曲的小车和起重机桥架上的台车销轴线在垂直平面内的同心度偏差要小于轨道中心距的0.15%,且最大不大于2 mm。参见图6。
图 6? 车轮形位偏差示意图
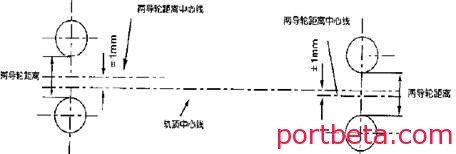
在同一轨道上滚动的车轮中心面同轨道中心的偏差,不得超过±1 mm,参见图7。
图 7? 车轮中心偏差示意图
如果采用水平导轮,则一个角上的导轮间距的中心同轨道中心线的偏差,不得大于±1 mm,参见图8。
图 8? 导向轮中心偏差示意图
1.2.2? 车轮的角偏差
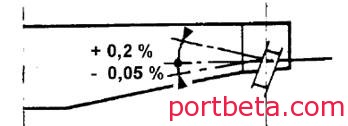
垂直方向上:如果轨道顶面是平直无曲率的,无载起重机的车轮轴线相对于水平面的倾斜度,必须在+0.2%~-0.05%之间,参见图9。
图 9? 车轮角偏差示意图
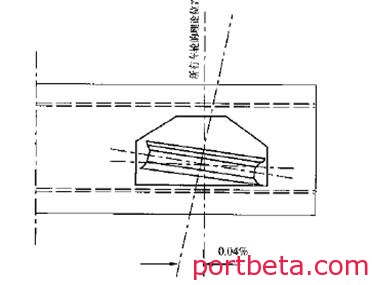
水平方向上:车轮孔中心同其理论中心线之间在水平面的角度偏差,不得大于±0.04%,可以这样理解,在车轮运行方向运行2 500 m的距离,车轮偏移起点位置1 m。显而易见,这个要求对车轮的装配及车架加工精度极为严格,参见图10。
图 10? 车轮水平面偏差示意图
当小车车轮由于加工、装配误差超出上述标准时,容易造成小车跑偏及啃轨现象,降低水平轮寿命,轨道过早磨损。
1.3? 小车跑偏的其它影响因素
对于自行式小车,各电机输出的转速、车轮直径的公差大小对小车运行都有一定影响。因此,在生产制作过程中需要严格控制。同样,码头场地的高低,也会对小车运行带来一定影响,这就需要根据具体情况,做一个系统的分析判断。
根据多年来的实践经验,大部分小车跑偏还是由于车轮轴孔镗孔偏差及装配不符合要求造成的。因此,对于小车的纠偏,主要是通过对小车车轮进行调整。
2? 车轮直线度的测量
对车轮精确的测量,得出角偏差及形位公差,是车轮跑偏调整的基础。
通过不断试验摸索,使用了徕卡TS 30超高精度全站仪对车轮的角偏差及形位公差进行测量。配合测量杆及反射棱镜,对车轮端面进行测量。
测量步骤如下:
1)设定徕卡坐标系,使徕卡坐标系内X坐标与前后两个车轮的安装基准线平行。
2)通过车架上的测量孔,对车轮的上下左右的轮缘位置进行测量。测量前,需要清理车轮测量面的油漆、油污等污染物,确保测量数据准确。一侧车轮测量完毕后,再测另一侧车轮的数据。
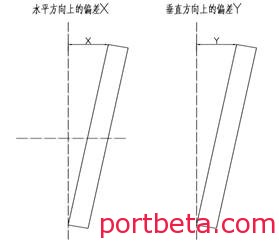
3)通过P 1,P 2的差值,得出车轮在水平方向的偏差X及垂直方向的差值Y,参见图11。
图 11? 车轮直线度测量示意图
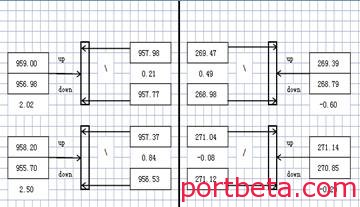
测量数据填入测量数据表,经过计算可以得到车轮的偏斜方向及偏斜量。参见图12-13。
图 12? 车轮偏斜量示意图
图 13? 车轮偏斜方向示意图
3? 车轮调整
3.1? 车轮结构形式分析
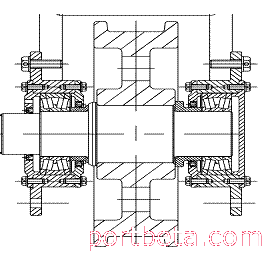
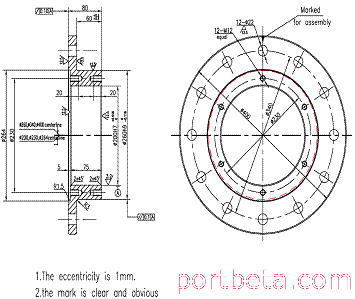
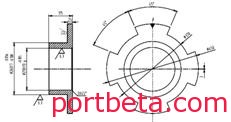
考虑到机加工精度及结构件累积误差等多种因素,车轮在设计过程中一般采用可调节形式弥补制作上的误差。在集装箱起重机上通常使用偏心套结构来进行调整。偏心套一般设计为12个调节螺栓孔,每个螺栓孔可以调节30°,通过左右两侧偏心套的角度组合,可实现车轮在水平面及垂直方向上偏斜,从而实现小车跑偏的调整。车轮结构形式,参见图14。
图 14? 车轮结构示意图
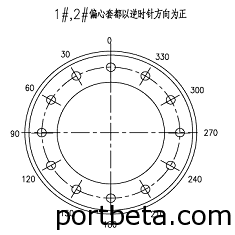
偏心套结构形式,参见图15。
图 15? 偏心套结构示意图
3.2? 偏心套的调整
在以往的调整过程中由于无法精确测量车轮偏斜值,因此无法计算出偏心套所需的调整量。只有通过不断的尝试摸索,才能得出一些经验值,但耗费大量的人力物力,无法推广普及。
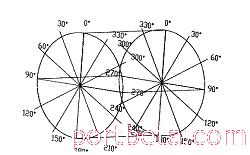
根据偏心套的结构及调整车轮的原理,通过公式计算,开发了EXCEL计算公式表,参见图16。
图 16? 车轮偏心套调整示意图
公式设定:
r为偏心距,D为车轮直径,L为偏心套#1、#2间距
θ1,θ2(θ1’ θ2’),分别为偏心套1和偏心套2沿逆时针方向的旋转角度
X车轮水平方向上的偏差,Y车轮垂直方向上的偏差
通过公式计算解得:

当车轮通过精确测量后,可以得到X,Y的偏差值,代入公式计算,即可得出偏心套理论上需要调整的角度,使车轮在水平方向上与垂直方向上的偏差趋近于零。
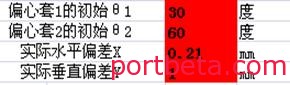
举例说明:偏心量为1 mm的偏心套,车轮直径500 mm,两偏心套之间的中心距289 mm,偏心套θ1初始角度为30°,偏心套θ2初始角度为60°。通过精确测量,得出车轮在水平方向上的偏差X为0.21 mm,在垂直方向上的偏差Y为1 mm,输入公式。
表 1? 初始角度
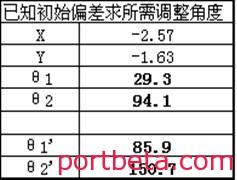
通过公式计算,得出偏心套#1的调整角度为29.3°,偏心套#2的调整角度为94.1°。由于偏心套分辨率为30°一个调节螺栓孔,因此,偏心套调整到最接近这个角度的位置,即30°和90°,这时,车轮在水平方向和垂直方向上的偏差最小。
表 2? 计算角度
根据现场调整经验在FEM规定的公差范围内,一般小车车轮成内八字形比两组相互平行的轮子更有利于小车按照直线方向运行,参见图17。
图 17? 内八字形布置好于相互平行的车轮
偏心套调整后,再开动一下小车,观察小车运行情况,根据现场实际运行情况,可再做一些微调。通过上述方法,在荷兰Euromax 轨道吊项目上运用,取得了良好的效果,大大缩短调整时间。
4? 结? 语
通过对标准的研究、小车结构的分析并结合精确测量和计算,对车轮跑偏以及偏心套的调整量有了定量的理论依据,一改以往凭经验摸索的调整方式,快速有效地解决了小车跑偏啃轨的问题。从而降低作业噪音,延长部件寿命,减少了维护保养成本,大大提高集装箱作业的效率。
在研究中发现,偏心套的可调分辨率越小,车轮的直线度调整越趋于精确。因此,经过设计部门的改进,开发了15°间隔的偏心套以及可任意角度调整焊接形式的偏心套,参见图18。
15°间隔的偏心套
可任意角度调整的偏心套
图 18
同样,这套理论计算公式稍加修改,也可以用于集装箱起重机偏心套形式的大车行走上,对解决大车跑偏及啃轨也有一定的参考价值。
参考文献
[1] F.E.M.标准欧洲起重机设计规范.(第3版 1998.10.1 第8章).
[2] ISO12488-1. Cranes-Tolerances for wheels and travel and traversing tracks.(First Edition.2005.04.15.
[3] GB/T.19683-2005.轨道式集装箱门式起重机.
[4] GB/T.14783-2009.轮胎式集装箱门式起重机.
[5] 附录:车轮偏心套角度调整计算公式.xls.