邱惠清卢凯良李雪归正曾怡
(同济大学机械工程学院上海,201804)
摘要:
基于神经网络随机模拟技术,对脉动风荷载作用下岸桥前大梁有限元模型动力学时域分析表明,前大果根部和销轴支座之间的间隙会增强前大梁的横向振动,并验证了脉动风荷栽是引起横向振动的主要原因。提出了在前大聚校支座处使用橡胶弹簧的弹性支承,以或小前大聚的横向振动,对比前大梁在无间隙、有间隙和橡胶弹簧支承下的动力学分析结果,当弹簧高度为20~30mm、硬度为40~60时,对减小前大梁振动的效果为佳,因大粱前端位移峰值较有间晾支承时下降了约10%,第3阶固有频率提高了17%左右,说明将前大粱饺支座支承改为弹性支承,对诚小岸桥前大粱横向振动的效果十分明显,
关健词:岸桥前大梁横向振动橡胶弹变支承脉动风载荷动力学分析 中图分类号:TH113.1
引言
岸桥前大粱由风荷载引起的横向振动不仅会对岸桥工作性能产生影响,而且还会对整机作业的安全性及寿命造成十分严重的危害。
目前,风工程的研究方法主要有:a,基于随机振动理论的理论分析法;b.现场实测;c,边界层风洞试验研究;d.以流体动力学为基础的数值算法。文献[1]对岸桥平均风荷载进行了风洞试验研究,获得了工作和非工作两种状态下主要构件在360°方向范围内的杆体型系数。文献[2]分析计算了圆截面斜撑杆在理想状态、实际运用状态及改进约束形式后的自振频率与相应的共振风速。此外,利用调质阻尼器抑制岸桥风致振动也可获得明显的效果)。
岸桥前大梁通过铰接方式与后大粱联结从而实现俯仰功能。但这种联结方式不可避免地会在大梁根部和销轴支座之间存有间隙。当前,国内在对岸桥的整机分析中常常忽略前大梁饺支座间隙的影响。本文旨在研究该间隙对大梁横向振动的影响,并提出在前大梁铰支座处使用橡胶弹簧填充间隙的弹性支承方式,以减小前大梁的横向振动。
1有间隙、无间隙支承情况下前大梁动力特性分析
1.1前大梁有限元模型的建立
本文研究的某岸桥前大梁为双箱粱,长为30m,高为1.5m,两根梁中心距为7.9m。由于主要研究大梁根部和销轴支座之间间隙对前大粱横向振动的影响,建立有限元模型时,忽略对横向刚度影响较小的拉索,在拉索铰点处施加位移约束,以保证大梁在自重和吊重下的平衡。
在无间隙支承下,选用BEAM189对前大梁有限元模型进行网格划分。大粱根部约束UX,UY,UZ和ROTX4个自由度,前大粱的有限元模型如图1所示。
前大粱在有间隙支承情况下,选用LINK8单元模拟间隙。在索杆结构分析中,常用LINK8模拟刚性杆,如果把材料的弹性模量设得非常小,则可用来模拟间隙,材料弹性模量越小越能近似间隙,但过小会造成施加荷载时大粱根部会穿透销轴支座。采用试算法时,选取满足施加风速为40m/s的风荷载时、大梁根部位移约为5mm这一条件的弹性模量来模拟间隙。经计算得弹性模量值取0.27MPa时大梁根部位移最接近该条件。
1,2前大梁模态分析比较
利用ANSYS模态分析模块可得到结构的模态分析结果,观察有、无间隙支承情况下前大梁前5阶振型表明,它们的前4阶模态性质相同。第1阶:前大粱在XZ水平面内的一阶弯曲:第2阶:前大梁在XY起升平面内一阶弯曲:第3阶:前大梁在XZ水平面内二阶弯曲,并伴随绕X轴轻微扭转:第4阶:前大梁绕X轴扭转:第5阶振型则完全不同。无间隙支承时,是前大梁在起升平面内二阶上下摆动;有间隙支承时,则为水平摆动,且呈正弦函数形状,并伴有微小的扭动。前大梁支承有、无间隙的前4阶固有频率及其比较见表1。
由表1可知,间隙对前大梁水平面内振动的第1,3阶固有频率的影响较大,尤其是对第3阶,这说明间隙对前大梁横向振动的影响较大。
1.3前大梁动力学分析及比较
前大粱风致动力响应分析的首要问题是脉动风荷载的随机模拟,即对作用在结构上的随机风场进行模拟)。文献[5]研究了大跨空间结构脉动风荷载的随机模拟技术,以神经网络作为线性滤波器进行了风速的随机模拟。并采用线性滤波器法中的自回归模型及其参数识别技术来模拟多维脉动风速时程,用两级3层BP神经网络分步实现脉动风速模拟。两级神经网络分别学习时间相关性和空间相关性知识。其模拟过程为:首先,进行BP神经网络训练,使其具有线性滤波器特性,学会模拟风荷载知识,并将这些信息存储在网络的连接权中。然后,使用训练好的BP神经网络进行脉动风速时程模拟,此时,只需输人人工产生的均值等于零,且具有白色谱的一系列随机数,BP神经网络就会自动生成具有给定时间相关性和空间相关性的数值风场。在风速时程的数值模拟中,水平风速谱采用Davenport的经验公式4)
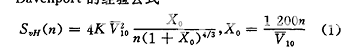
其中:n为脉动风频率(Hz);K为地面粗糙度系数;V.为离地面标准高度10m处的平均风速(m/s),取B类地貌的基本风压为0.45kN/m2.利用上述方法,可得到顺风向水平脉动风速时程曲线,经适当简化后得到水平风速时程曲线(见图2)中的0~70s部分。为了比较前大梁在平均风荷载作用下的动力响应,70s后取基本风速为20m/s的平均风。
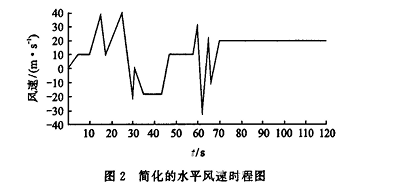

在ANSYS中添加荷载步进行迭代求解,得到有间隙、元间隙支承情况下前大梁前端节点的Z向变形最大位移时程曲线,如图3所示。可见,脉动风荷.
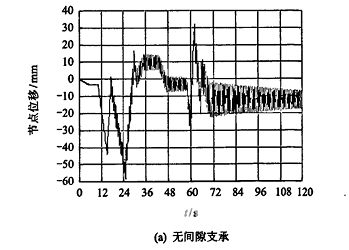
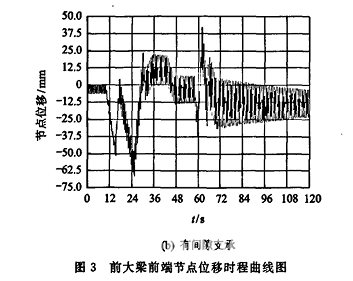
载是引起前大梁横向振动的主要原因,间隙的存在使前大梁在风荷载作用下振幅明显增大。在脉动风荷载作用下,有间隙支承比无间隙支承的最大位移振幅增加了13.2%。因此,希望通过改进支承的方式,既能减小振幅和前大粱根部支承反力,又不影响起重机工作时前大梁的俯仰。
2弹性支承减隔振效果
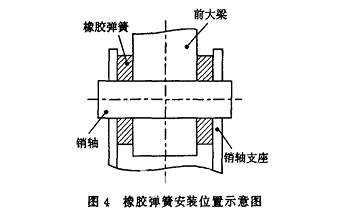
近年来,橡胶弹簧在工程中的应用日益广泛,因其具有优点:a.形状不受限制,刚度可以根据设计要求自由选择;b,具有高弹性、良好的耐磨性和阻尼特性:℃.安装和拆卸方便,无需润滑,有利于维护和保养。本文选择用橡胶弹簧弹支承来代替间隙支承,并安装在前大梁根部与支座之间(见图4)。
2.1橡胶弹簧的设计
天然胶综合物理机械性能比较优越,其压缩刚度

其中:A为橡胶受压截面面积;^为弹簧高度。
橡胶的表观弹性模量

其中:i为表示几何形状影响系数,对于圆环截面,

可见,橡胶弹簧的刚度与橡胶硬度、截面形状和弹簧高度有关[8]。改变弹簧的高度及硬度,计算所得的表观弹性模量见表2。
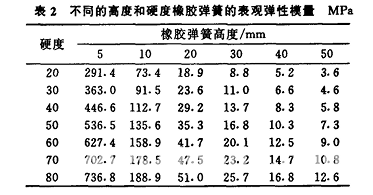
2.2弹性支承情况下前大梁模态分析
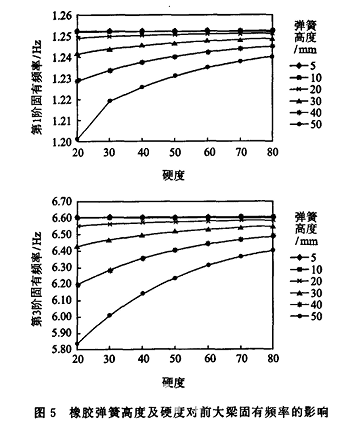
由前述第1.2节模态分析结果可知,第1,3阶模态反映前大梁的水平振动。因此,对于安装了橡胶弹簧后的前大梁亦可只关注其第1,3阶的固有频率,其计算结果见表3。

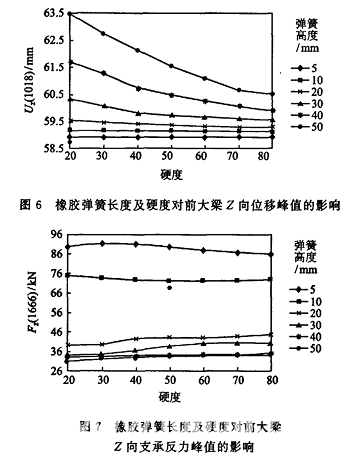
橡胶弹簧高度和硬度对前大梁固有频率的影响见图5。可见,用橡胶弹簧作为弹性支承,可在一定程度上提高前大梁的固有频率。当弹簧高为5mm,硬度为80时,弹性支承的固有频率值最大,已经非常接近无间隙支承时的值。
2.3弹性支承情况下前大梁动力学分析
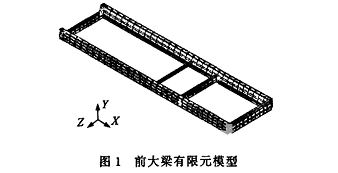
弹性支承时前大梁的动力学分析方法与前述第1.3节同。计算后得到前大梁最前端节点1018的Z向位移峰值Uz和根部节点1666的支承反力峰值Fz随橡胶弹簧长度及硬度变化,分别见图6和图7。