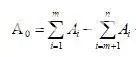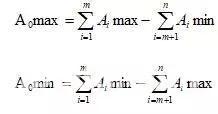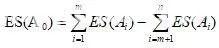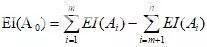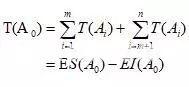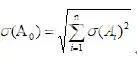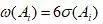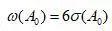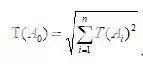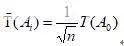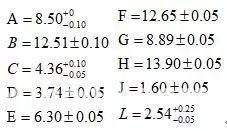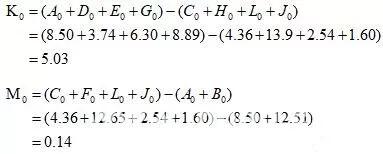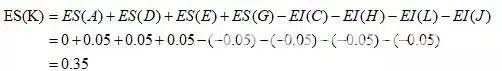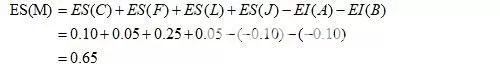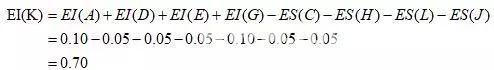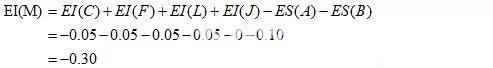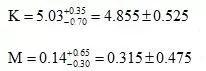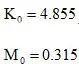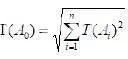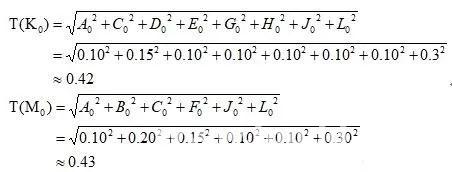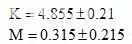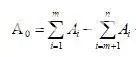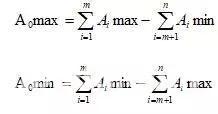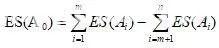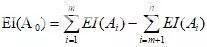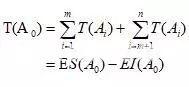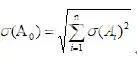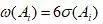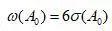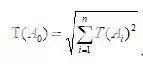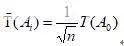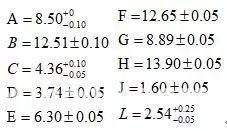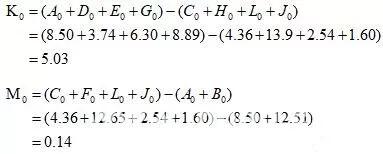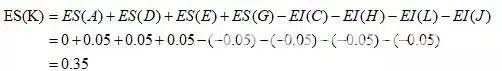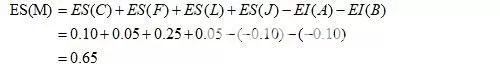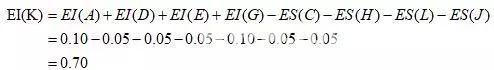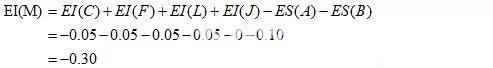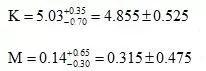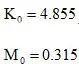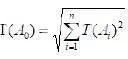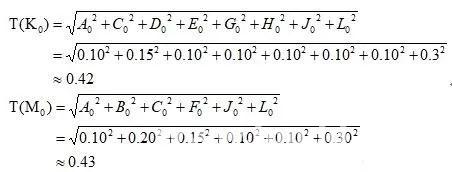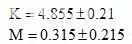尺寸链计算与公差分析的目的
检查工艺漏洞,提前优化,避免试生产造成的资源及时间浪费;
尺寸链是由一组相互连接的尺寸形成的封闭尺寸组。在工程设计和制造中经常用尺寸链来进行工艺尺寸换算,控制关键尺寸的公差,从而保证产品的制造精度。
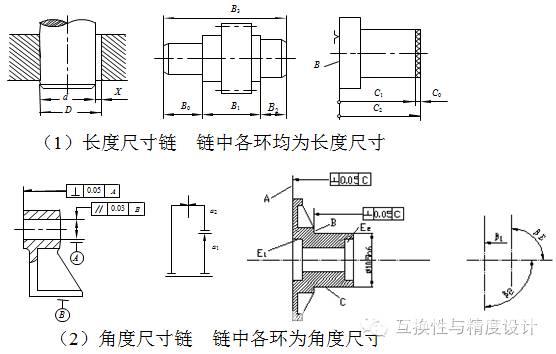
◆ 按其空间位置的构成可以分为:线性尺寸链(一维)、平面尺寸链(二维)和空间尺寸链(三维)。
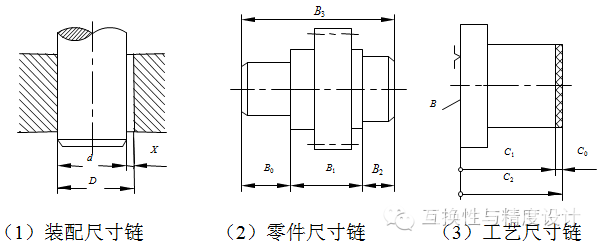
◆ 按其功能可以分为:装配尺寸链、零件尺寸链和工艺尺寸链。
在零件的加工过程中,决定各个工序要素间相互关系的尺寸通常可用彼此相联系的点、线、面按一定顺序排列,形成一个封闭的尺寸系统,这个尺寸系统就称为工艺尺寸链。
由于产品的复杂性,产品制造需要很多工序才能完成。由于加工基准的转换,使工艺尺寸换算在工艺设计过程中占有非常重要的地位。尺寸换算主要有以下几种形式:
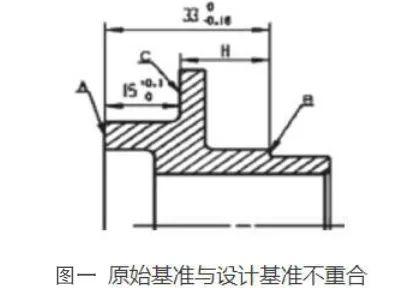
图1中A为设计基准,B为加工面,C为原始基准,尺寸H必须通过换算后求出。
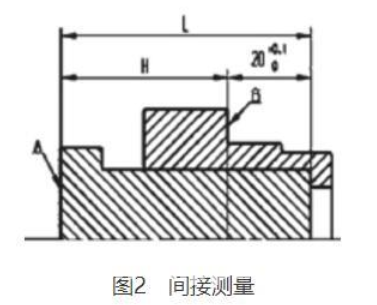
图2中工序原始尺寸为20,B为加工面。若要对该尺寸直接测量比较困难,因此将一个芯轴安装在零件上,与零件内部的定位面接触,借助基准A进行间接测量。尺寸L为固定长度,因此可以通过测量H来间接保证工序尺寸为20。
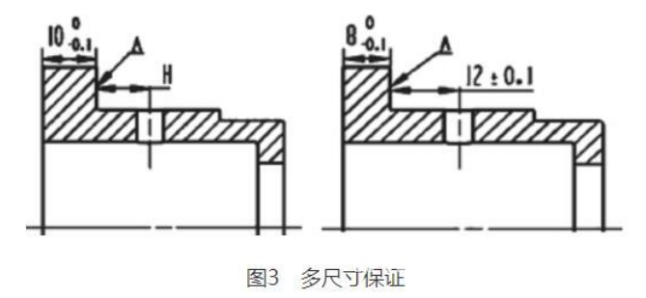
图3中小孔在粗加工阶段已经加工完成,主设计基准A在最后面加工保证,与主设计基准有关的尺寸有4个:10、H、8、12。两个工序中,小孔中心与左端面的距离不变,因此H值由10、8、12 三个尺寸共同来保证。
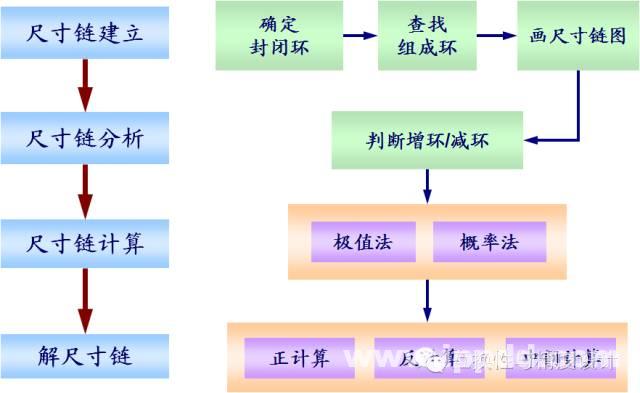
工艺尺寸链的解算步骤由上所述,要利用尺寸链原理来分析相互关联的工序尺寸及余量的变化规律。首先要由零件工序图画出尺寸链图,然后找出封闭环、增环、减环等进行解算。解算关键在于能否正确地画出尺寸链,判断封闭环。对于在生产实践中已出现和未出现的复杂尺寸链解算问题,都需要根据尺寸链的定义及工艺目的进行准确把握,再根据实际情况来进行解算。
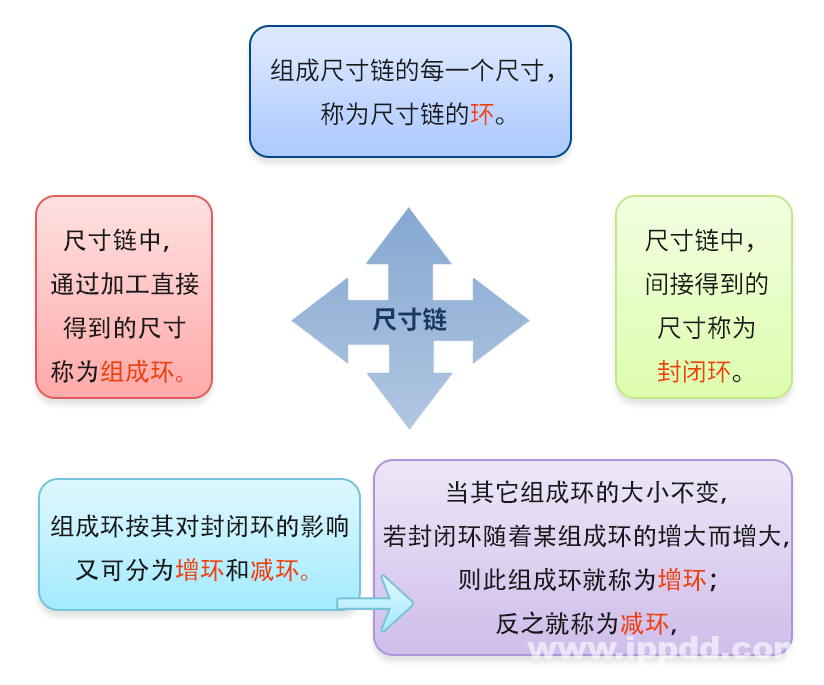
尺寸链的定义:由产品设计或工艺要求所确定的某一尺寸和对该尺寸有直接影响的全部尺寸,连接形成的封闭尺寸组。
尺寸链具有封闭性和相关性:尺寸链一定是封闭的,尺寸链中各尺寸一定具有相互联系。
封闭环:加工或装配过程中最后自然形成的尺寸叫做封闭还。封闭环常用下标为“0”的字母表示 。一个尺寸链中只有一个封闭环。判断封闭坏是尺寸链分析的最重要一步。
组成环:除封闭环以外的其他环叫做组成环。组成环通常用下标为“1,2,3,…”的字母表示。根据对封闭环的影响不同,组成环分为增环和减环。
增环:与封闭环同向变动的组成环称为增环。即其他组成环不变,该组成环尺寸增大(或减小),封闭环尺寸随之增大(或减小)。
减环:与封闭环反向变动的组成环称为减环。即其他组成环不变,该组成环尺寸增大(或减小),封闭环尺寸随之减小(或增大) 。
按照形成原因,尺寸链分为装配尺寸链、零件尺寸链和工艺尺寸链。 按照空间布置,尺寸链分为直线尺寸链、平面尺寸链和空间尺寸链。
试切法是指操作工人在每个工步或走刀前进行对刀,然后切出一小段,测量其尺寸是否合适,如果不合适,将刀具的位置调整一下,再试切一小段,直至达到尺寸要求后才加工全部表面。通过试切—测量尺寸—调整刀具的吃刀量—走刀切削—再试切,如此反复直至达到所需尺寸。此法主要用于单件小批生产。
调整法是一种加工前按规定的尺寸调整好刀具与工件相对位置及进给行程,从而保证在加工时自动获得所需距离尺寸精度的加工方法。这种加工方法在加工时不再试切。生产率高,其加工精度决定于机床、夹具的精度和调整误差,用于大批量生产。
极值法适用于试切法加工,加工后的工件尺寸偏向于最大实体尺寸,极值法考虑工件处于极限偏差时对封闭环造成的影响。
概率法适用于调整法加工,加工后的工件尺寸以公差带为中心呈正态分布,概率发考虑工件处于公差带中心时对封闭环造成的影响。
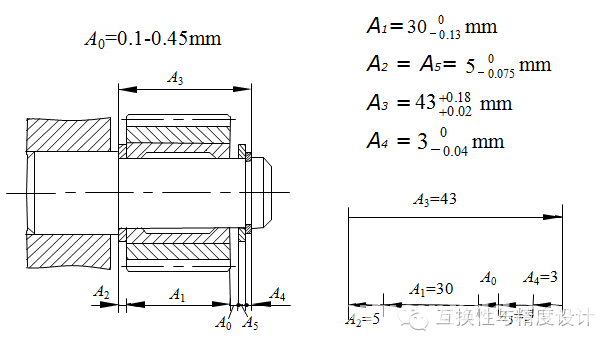
例1. 已知如下图所示的齿轮部件装配,轴是固定不动的,齿轮在轴上回转,要求齿轮与挡圈的轴向间隙为0.1-0.45 mm。试采用完全互换法装配,试确定各组成环公差和极限偏差。
凡是改变生产对象的形状、尺寸、相对位置和性质等,使其成为成品或半成品的过程成为工艺过程。
而机械制造工艺过程是指零件的机械加工工艺过程和成品的装配工艺过程。
为方便分析机加工的情况和制订工艺过程,将工艺过程分成若干工序,工序分成若干工步,工步分成若干工工作行程。其细分依实际需求而定。
所谓工序是指:相同的工作人员在相同的工作地点对同一工件所完成的那一部分工艺过程。
所谓工步是指:相同加工工具对同一工件在相同加工条件下所连续完成的那一部分工序。
所谓工作行程是指:加工工具在工件上一次所完成的工步部分。
如果工艺过程中只有一道工序,工序中又只有一步工步,工步由一个工作行程组成,那么它们实际是相当的。
将工艺过程的操作方法等按一定的格式用文件的形式规定下来,便形成了工艺规程,即SOP。
加工工艺过程中,治具及工件的实际位置必然会与理想定位位置有一定的差异,同时加工尺寸亦会存在差异,需允许一定的误差存在,如何确定其误差符合要求,则需引入尺寸链及公差的概念,并进行分析计算。
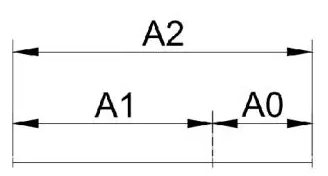
互相联系的尺寸按一定顺序首尾相接形成封闭的尺寸组。(如图)
关联性:尺寸链中间接保证的尺寸大小和变化,受到直接获得
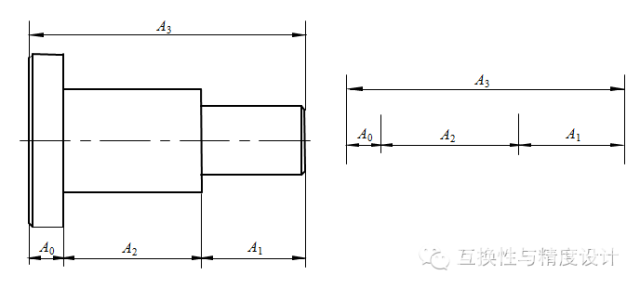
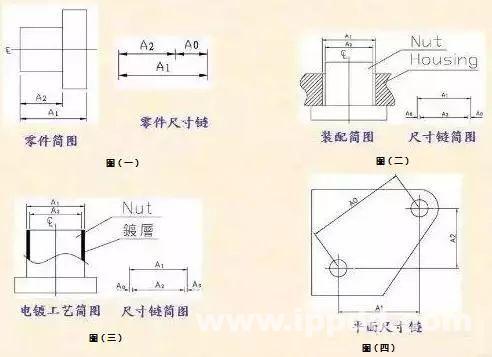
零件尺寸链:由几个设计尺寸所形成的尺寸链。如图(1)
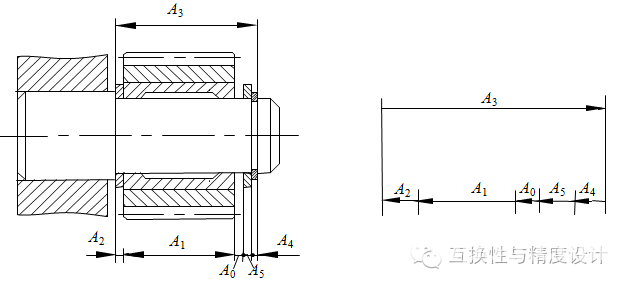
装配尺寸链:由不同零件的尺寸所形成的尺寸链。如图(2)
工艺尺寸链:同一个零件的工艺尺寸所形成的尺寸链。如图(3)
直线尺寸链:是全
按照空间布置,尺寸链分为直线尺寸链、平面尺寸链和空间尺寸链。
试切法是指操作工人在每个工步或走刀前进行对刀,然后切出一小段,测量其尺寸是否合适,如果不合适,将刀具的位置调整一下,再试切一小段,直至达到尺寸要求后才加工全部表面。通过试切—测量尺寸—调整刀具的吃刀量—走刀切削—再试切,如此反复直至达到所需尺寸。此法主要用于单件小批生产。
调整法是一种加工前按规定的尺寸调整好刀具与工件相对位置及进给行程,从而保证在加工时自动获得所需距离尺寸精度的加工方法。这种加工方法在加工时不再试切。生产率高,其加工精度决定于机床、夹具的精度和调整误差,用于大批量生产。
极值法适用于试切法加工,加工后的工件尺寸偏向于最大实体尺寸,极值法考虑工件处于极限偏差时对封闭环造成的影响。
概率法适用于调整法加工,加工后的工件尺寸以公差带为中心呈正态分布,概率发考虑工件处于公差带中心时对封闭环造成的影响。
例1. 已知如下图所示的齿轮部件装配,轴是固定不动的,齿轮在轴上回转,要求齿轮与挡圈的轴向间隙为0.1-0.45 mm。试采用完全互换法装配,试确定各组成环公差和极限偏差。
凡是改变生产对象的形状、尺寸、相对位置和性质等,使其成为成品或半成品的过程成为工艺过程。
而机械制造工艺过程是指零件的机械加工工艺过程和成品的装配工艺过程。
为方便分析机加工的情况和制订工艺过程,将工艺过程分成若干工序,工序分成若干工步,工步分成若干工工作行程。其细分依实际需求而定。
所谓工序是指:相同的工作人员在相同的工作地点对同一工件所完成的那一部分工艺过程。
所谓工步是指:相同加工工具对同一工件在相同加工条件下所连续完成的那一部分工序。
所谓工作行程是指:加工工具在工件上一次所完成的工步部分。
如果工艺过程中只有一道工序,工序中又只有一步工步,工步由一个工作行程组成,那么它们实际是相当的。
将工艺过程的操作方法等按一定的格式用文件的形式规定下来,便形成了工艺规程,即SOP。
加工工艺过程中,治具及工件的实际位置必然会与理想定位位置有一定的差异,同时加工尺寸亦会存在差异,需允许一定的误差存在,如何确定其误差符合要求,则需引入尺寸链及公差的概念,并进行分析计算。
互相联系的尺寸按一定顺序首尾相接形成封闭的尺寸组。(如图)
关联性:尺寸链中间接保证的尺寸大小和变化,受到直接获得
零件尺寸链:由几个设计尺寸所形成的尺寸链。如图(1)
装配尺寸链:由不同零件的尺寸所形成的尺寸链。如图(2)
工艺尺寸链:同一个零件的工艺尺寸所形成的尺寸链。如图(3)
直线尺寸链:是全
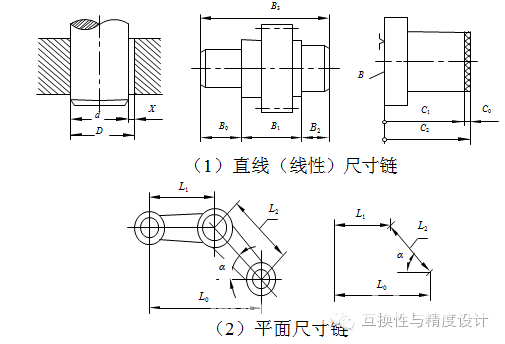
部组成环平行于封闭环的尺寸链。如图(1),(2),(3)
平面尺寸链:全部组成环位于一个或几个平行平面内,但某些组成环不平行于封闭环的尺寸链。如图(4),两孔之间的尺寸构成了一平面尺寸链。
增环:当其余组成环不变,封闭环因其增大而增大的环。
减环:当其余组成环不变,封闭环因其增大而减少的环。
以封闭环开始,按“最少组成环环数”的原则,画出实际组成环。
按各尺寸首尾相接的原则,顺着一个方向在各尺寸链终端箭头,凡是箭头方向与封闭环箭头相同的尺寸就是减环,反之就是增环。
工艺尺寸链的构成,取决于工艺方案和具体的加工方法。
概率法:应用于生产批量大的自动化及半自动化生产方面,或尺寸链的环数较多的场合。
A0:封闭环的基本尺寸,m为增环数,n-m为减环数
A.按等公差值的原则分配封闭环公差(计算上方便,工艺上不合理)
B:按等公差级的原则分配封闭环的公差(按基本尺寸大小来分配公差,工艺上较合理)
按具体情况分配,这与设计经验相关,实质上就是从工艺观点考虑。
根据概率论,可得组成环Ai与封闭环A0三者的均方根误差关系式:
因为对于正态分布,其偶然误差ω即尺寸分散带与均方根偏差σ间的关系可取ω=6σ,从而各组成环的尺寸分散带为
若T(Ai)的平均值基本上满足经济精度的要求,则可按组成环加工的难易程度合理调配公差。概率法的好处是求得的组成环公差比极值法的要求大√n倍。
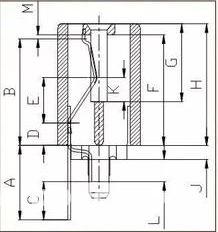
图中有两封闭环尺寸K、M,其中封闭环K的增环有A、D、E、G,减环有C、H、L、J;封闭环M的增环有C、F、L、J,减环A、B
-End-
免责声明:本文系网络转载或改编,未找到原创作者,版权归原作者所有。如涉及版权,请联系删。