有效配合过盈量是指工作中实际起作用的配合过盈量,它是设计过盈量受各种因素的影响发生变化形成的。
有效过盈量与多种因素有关,如离心膨胀、热膨胀、配合表面粗糙度、几何形状误差等。
其计算式可表示为
Δf=Δfo+Δfc+Δft+Δfq
式中,
Δf–为有效过盈量;
Δfo–为原始设计过盈量;
Δfc–为内圈和轴的离心膨胀引起的过盈量变化或外圈与轴承座的离心膨胀量引起的过盈量变化;
Δft–为热膨胀引起的过盈量变化;
Δfq–为粗糙度、几何误差等其它原因引起的过盈量变化
因为高速轴承需要考虑离心膨胀引起的过盈量变化,之前因素已经分析过,本次只分析离心膨胀引起的过盈量变化
1、外圈与轴承座因转速引起过盈量变化
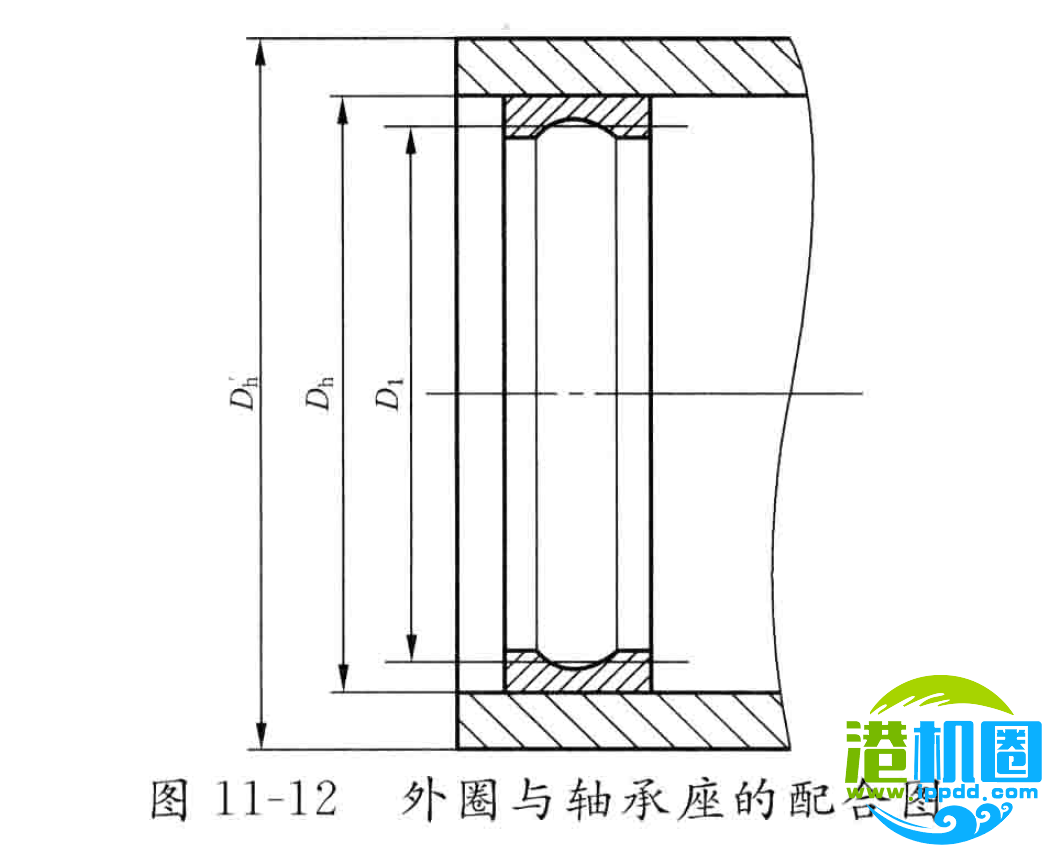
外圈与轴承座的配合如图11-12,D1为外圈的平均内径,即挡边直径与沟底直径的平均值。
因转速引起的配合直径的增量为:
Δfco=(2*ρ1*R13*Ω12*10-9)/E1-(2*ρh*Rh3*Ω12*10-9)/Eh
式中:
计算结果:正值表示外圈的离心增量大于轴承座离心增量,表示轴承座与外圈过盈量增大
负值表示外圈的离心增量小于轴承座离心增量,表示轴承座与外圈过盈量减小
Δfco–过盈量(mm)
ρh–轴承座的密度(g/cm2)
ρ1–轴承外圈的密度(g/cm2)
Eh–轴承座的弹性模量(MPa)
E1–轴承外圈的弹性模量(MPa)
Ω1–轴承外圈与轴承座的转速(rad/s)
Rh=0.25*(Dh’+Dh)(mm)
R1=0.25*(Dh+D1)(mm)
2、内圈与轴因转速引起过盈量变化
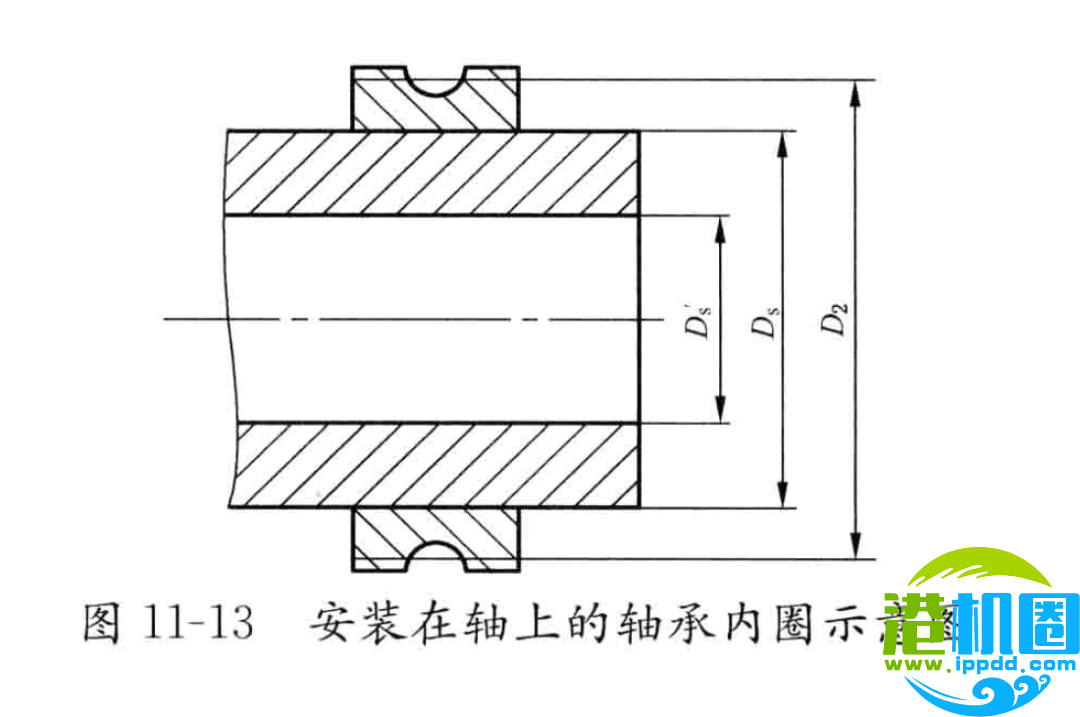
内圈与轴颈的配合如图11-13,D2为内圈的平均外径,即挡边与沟底的平均直径。
Δfci=(2*ρs*Rs3*Ω22*10-9)/Es-(2*ρ2*R23*Ω22*10-9)/E2
式中:
计算结果:正值表示轴的离心增量大于内圈离心增量,表示内圈与轴过盈量增大
负值表示轴的离心增量小于内圈离心增量,表示内圈与轴过盈量减小
Δfci–过盈量(mm)
ρs–轴的密度(g/cm2)
ρ2–轴承内圈的密度(g/cm2)
Es–轴的弹性模量(MPa)
E2–轴承内圈的弹性模量(MPa)
Ω2–轴承内圈与轴的转速(rad/s)
Rs=0.25*(Ds’+Ds)(mm)
R2=0.25*(Ds+D2)(mm)
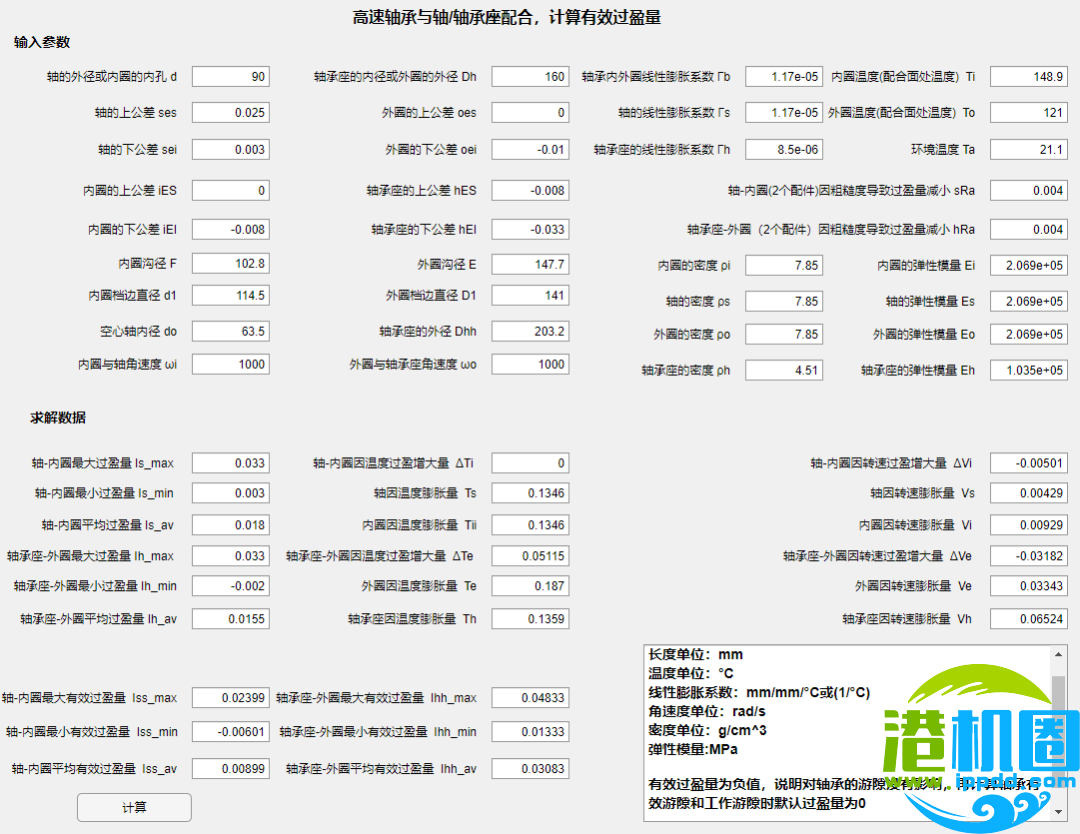
例 218ACBB角接触球轴承内径为90mm,外径为160mm,加工精度为ABEC-7级。轴承与孔径为63.5mm的空心钢轴按k6配合;与有效外径为203.2mm的钛轴承座按M6配合。角接触球轴承内圈平均工作温度为148.9°C,外圈为121°C,室温为21.1°C,轴承内圈档边直径114.5mm,内圈沟径102.8mm,外圈档边直径141mm,外圈沟径147.7mm,轴承和轴密度为7.85g/cm^3,轴承座密度为4.51g/cm^3,轴承和轴弹性模量206900MPa,轴承座弹性模量103500MPa,假定轴承内圈与轴转速为1000rad/s,外圈与轴承座的转速为1000rad/s,确认轴-内圈,轴承座-外圈有效的过盈量是多少